一句话来说,布隆过滤器是为了 解决集合中是否存在某一元素 这一问题。
这种需求非常常见,比如现有 500 万个电话号码,给你 1 万个电话号码,如何要快速准确的判断这些电话号码是否已经存在?
什么是 Bitmap?
Bitmap(位图),顾名思义,是一种以二进制位(bit)来表示数据的特殊数据结构。
在编程中,我们往往需要记录某种状态,比如签到系统中的 用户签到状态,答题中的每道题作答状态,对于这种只有两种情况的状态,如果使用传统的数据结构,往往需要非常多的存储空间;
比如我们使用用户 id 来存储用户状态,比如使用 java 中的 int,每个 id 就需要 4 字节的存储空间;但是 Bitmap 通过将每一个状态(0或1)直接映射为一个位,就大大的节省了空间。
BitMap 有这些优点:
- 空间效率很高,假设要存储一亿个用户的状态,使用 Bitmap 就只占用 12MB 的存储空间。
- 查询速度快,不管查询哪个数据,都只需要 O(1) 的时间复杂度。
- 简单易用,看了上面的介绍,大家应该也能实现一个简单的 Bitmap 了,在使用中,也只是简单的插入、查找、删除指令。
但是,Bitmap只能表示两种状态,不适合需要更多状态表示的场景。
此外,若数据稀疏(如仅有几个特定位被设置),则可能导致浪费存储空间,比如上面一亿用户的例子,可能只有几个人的状态被记录,那就会大量浪费空间。
布隆过滤器(Bloom Filter)
什么是布隆过滤器
「Wiki-Bloom filter」:https://en.wikipedia.org/wiki/Bloom_filter
如果我们有一个 10 万位的 Bitmap,此时突然需要我们记录一个序号为一亿的状态,我们要将 Bitmap 拓展到一亿位吗?
这显然是不可取的,但是,可以通过 hash 函数将这个记录映射成 10 万以内的数据就解决了。
但只要有哈希,就有哈希碰撞,而只要有哈希碰撞就必然会引起误判,那有没有方法能够减弱这种误判呢?
很简单,一个哈希不行,我可以用两个,两个不行我可以用三个。。。
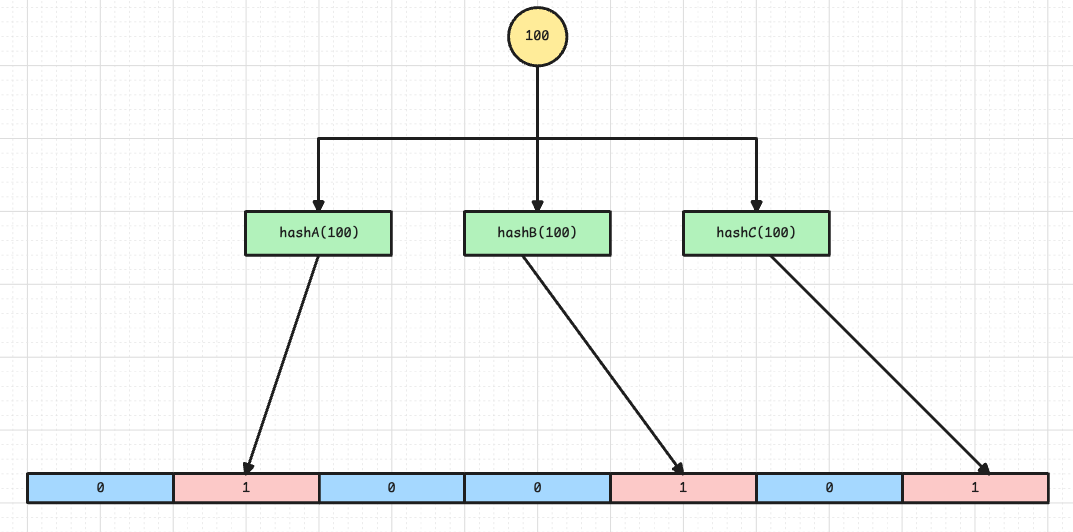
布隆过滤器正是这样做的,通过 多个哈希函数,将数据映射到多个不同的索引位置,然后将这些索引位置通通置为 1,检查的时候,如果几个位置都为 1,那就说明元素肯定在库中。
但这样无法完全避免误判,比如有三个哈希函数,而一个不存在的元素映射的三个位置都被置为 1,这也是有可能的,但这种概率已经被降到了很小。
那,究竟有多小呢?
布隆过滤器的误判率是多少?
假设布隆过滤器的数组长度为 $m$,插入元素的个数为 $n$,使用哈希函数的个数为 $k$。
对于一个特定的位,在插入一个元素时被置为 1 的概率为 $p = 1/m$。
插入 $n$ 个元素后,这个位仍然为 0 的概率为 $(1 - p)^{kn}$。
那么这个位为 1 的概率就是 $1-(1 - p)^{kn}$。
当查询一个不在集合中的元素时,如果确定其存在的话,对于每个哈希函数对应的位都应该为 1,$P=(1-(1 - p)^{kn})^{k}$。
将 $p = 1/m$ 代入上式,可得 $P=(1-(1-\frac{1}{m})^{kn})^{k}$。
对结果进行分析可以得知,数组长度越高,哈希函数越多的话,误判率越低,也非常符合我们的直觉。
因为 $m$ 的值,也就是布隆过滤器的容量可以非常大,可以近似认为趋近于 $+\infty$,此时上式可以视为 $P \approx (1 - e^\frac{-kn}{m})^k$
绝大多数的时间,我们关注的都是误判率和插入元素的个数,即 $P$ 和 $n$,所以我们希望能够指定这两个个数,然后通过计算得出哈希函数的个数 k 和数组长度 m
通过数学分析,我们可以发现,当
$k = \frac{m}{n} \ln 2$ 时,误判率 P 最小,将这个值代入上面的式子,简化指数项,可以得出 $P \approx \left( 1 - \frac{1}{2} \right)^{\frac{m}{n} \ln 2}$
进而得出: $P \approx \left( \frac{1}{2} \right)^k$
可以推导出 $P$ 和 $k$ 的关系,为:$k = -\frac{\ln P}{\ln 2}$
将这个式子代入 $k = \frac{m}{n} \ln 2$,可以得出 $m$ 和 $p$ 的关系,$m = \frac{n\ln P}{(\ln 2)^2}$
布隆过滤器的优缺点
首先,它是由 bit 数组来构成的,所占空间小。
和 Bitmap 相同,其插入和查询的时间复杂度均为 O(1)。
但是相较于 Bitmap,只要使用哈希,就不可避免的存在误判,所以布隆过滤器存在误判,但是通过合理的参数配置,误判率可以控制在一个可接受的范围内。
同时,布隆过滤器不允许删除元素,如果简单的将所有哈希函数计算出来的索引位置全部置为 1 的话,会引起大范围的误删。
Guava 提供的布隆过滤器实现
「GitHub地址」:https://github.com/google/guava
Guava,Google Java Core Libraries,是谷歌开发的 Java 核心库。
写一个简单的案例来延时一下 Guava 提供的布隆过滤器,测试环境为 jdk1.8;
| |
创建布隆过滤器,依靠的是 com.google.common.hash.BloomFilter 类提供的 create() 方法,这个方法接受三个参数,分别是:
- Funnel:负责将对象转为一系列字节的工具接口,即指定布隆过滤器中要存放什么类型的对象。
- expectedInsertions:期望插入的元素个数。
- fpp:期望的误判率。
| |
测试类,在主方法中,我们通过反射来查看一下 Guava 生成的布隆过滤器哈希函数个数和数组长度:
| |
| |
输出结果为:
| |
根据「布隆过滤器的误判率是多少?」部分的推导,相信大家对通过 期望插入元素的个数 以及 期望预判率 是计算 bit 数组长度和哈希函数个数的方法有所了解了,这里我们来尝试计算一下:
- 首先计算位数组长度 $m$:
- 根据公式 $m = -\frac{n * \ln{p}}{(\ln{2})^2}$,其中$n = size = 1000000$,$p = fpp = 0.01$。
- 先计算$\ln{p}=\ln{0.01}\approx -4.60517$。
- 再计算$(\ln{2})^2\approx0.4804530139182014$。
- 则 $m = -\frac{1000000 * (-4.60517)}{0.4804530139182014}\approx9585059.539989209$。
- 接着计算哈希函数个数 $k$:
- 根据公式 $k = \frac{m}{n} * \ln{2}$,其中$m\approx9585059.539989209$,$n = 1000000$。
- 先计算 $\ln{2}\approx0.6931471805599453$。
- 则 $k=\frac{9585059.539989209}{1000000} * 0.6931471805599453\approx6.643859708244697$,取整为 $7$。
最终计算得出,位数组长度约为 $9585059.539989209$,哈希函数个数为 $7$,和测试结果完全吻合。
布谷鸟过滤器:Cuckoo Filter
什么是布谷鸟过滤器?
「Cuckoo Filter: Practically Better Than Bloom」:https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf
「GitHub 地址」:https://github.com/efficient/cuckoofilter
「Wiki-Cuckoo filter」:https://en.wikipedia.org/wiki/Cuckoo_filter
下面的部分来自对 GitHub 梗概部分的简单翻译:
布谷鸟过滤器(Cuckoo filter)是一种用于近似集合成员查询的布隆过滤器替代方案。
布隆过滤器是众所周知的节省空间的数据结构,适合用于回答“元素 x 是否在集合中?”这样的查询。但布隆过滤器不支持删除操作。为了支持删除功能,布隆过滤器的一些变体(如计数布隆过滤器)通常需要更多的存储空间。
布谷鸟过滤器提供了灵活的动态添加和删除元素的能力。布谷鸟过滤器基于布谷鸟哈希(因此命名为布谷鸟过滤器)。它本质上是一个布谷鸟哈希表,存储每个密钥的指纹。
布谷鸟哈希表可以非常紧凑,因此 cuckoo 过滤器可以比传统的布隆过滤器使用更少的空间,且适用于需要低误报率 (< 3%) 的应用程序。
可以看出,布谷鸟在布隆过滤器的基础上,提供了 删除 的能力,而且还优化了空间和效率。
布谷鸟过滤器是如何支持删除的?
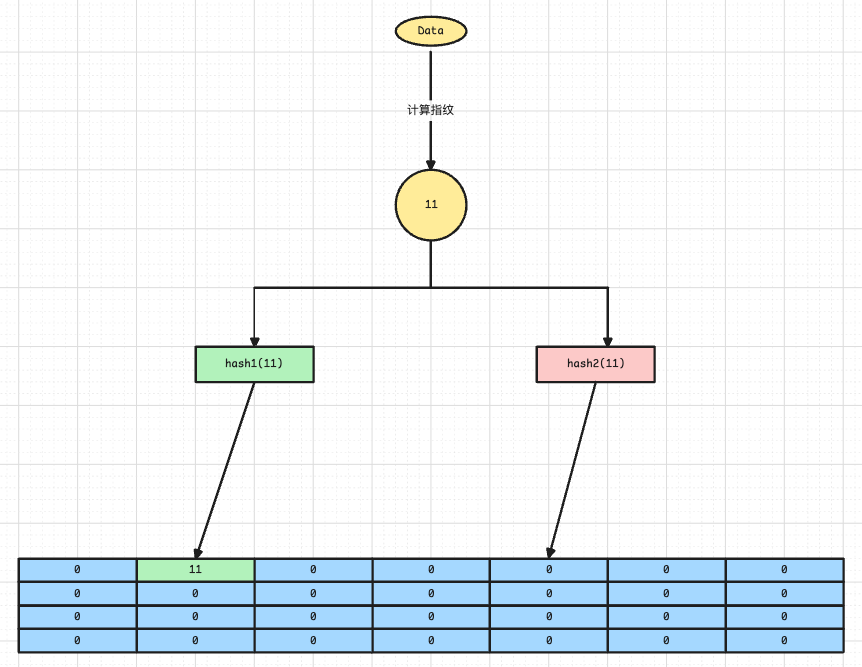
如上图所示,布谷鸟过滤器由三部分组成:哈希表、存储在哈希表中的指纹和两个不独立的哈希函数。
既然要删除元素,将不可避免的要去存储这个元素或者说存储某个标识,在布谷鸟过滤器中,这个元素的标识被称为指纹(fingerprint),当删除的时候,只需要删除这个元素的指纹就可以了。
布谷鸟过滤器的实现原理
在 GitHub 官网中提到,布谷鸟过滤器对外提供了这些 API:
| |
插入(Add)
采用伪代码的形式,插入的流程是这样的:
| |
与布隆过滤器使用 bit 数组不同的是,布谷鸟过滤器使用的是哈希数组,某一个位置(Bucket)可以存储多个指纹,只有当这个 Bucket 完全被填满了之后,再去尝试其他的方法。
当一个元素x要插入到布谷鸟过滤器时,布谷鸟过滤器会先使用fingerprint函数计算出指纹fp,接着用 hash1 算法对计算式第一个桶位置 p1,然后尝试将指纹插入到 p1 的位置;
如果插入失败的话,再次通过 hash2 函数,传入 p1 和 fp,然后尝试将指纹插入到 p2 位置。
但如果 p2 位置也满了的话,就会触发布谷鸟过滤器的驱逐(kickout)机制,它会将这个桶中随机的一个元素踢出去,然后直接鸠占鹊巢;
被踢出去的这个元素再次去尝试上面的步骤,继续寻找位置、尝试插入、驱逐、寻找位置。。。
但这个过程不是无穷无尽的,当尝试的次数达到某个上限的时候,布谷鸟过滤器就会认为自己已满。
口说无凭,我们直接来看一下布谷鸟过滤器的源码:
| |
- 首先通过
victim_.used判断是否为满,为什么可以判断放到后面去讲解。 - 然后通过
GenerateIndexTagHash生成下标 1 和指纹。 - 调用
AddImpl将元素添加到哈希表中。
| |
上面列出的就是插入元素的具体实现
- 如果第一次就插入成功,也就是
table_->InsertTagToBucket(curindex, curtag, kickout, oldtag)语句执行成功,直接返回OK。 - 如果第一次没有插入成功,接下来的插入操作都将进入驱逐模式,即如果没有空位置,就将原位置的元素直接踢出,
InsertTagToBucket(curindex, curtag, kickout, oldtag)将会将oldtag设置为踢出的元素,然后继续执行插入操作。 - 如果到最后还是没有成功,可以视为过滤器已经满了,此时
victim_.used = true;,这也是为什么上面可以通过victim_.used来判断过滤器是否满的原因。
| |
插入方法:InsertTagToBucket,
先尝试在索引位置插入元素,如果插入失败,且当前不是驱逐模式,直接返回;
如果当前是驱逐模式,将随机一个元素存储在 oldtag 中,然后将元素插入到那个位置
| |
AltIndex 函数根据计算出的主索引 index 和标签 tag 计算一个替代索引。它通过对主索引 index 和标签 tag 乘以一个常数 0x5bd1e995 后进行异或(^)运算,再通过 IndexHash 计算出替代位置。
相比于之前的异或操作(也是现在网上大部分的解释),这种做法在实现简单的同时依然具有良好的分布特性,确保元素能在较小的表中分布均匀,同时这个操作是可逆的,即通过 p2 也能得到 p2。
查询是否存在(Contain)
看懂了 Add 方法,后面就非常容易理解了:
| |
上面的方法就是计算 i1 和 i2,然后去这两个位置寻找,如果存在的话,返回 true。
found = victim_.used && (tag == victim_.tag) && (i1 == victim_.index || i2 == victim_.index); 是为了在过滤器满了之后插入的那个元素可以被检索到。
删除操作(Delete)
| |
还是先生成两个索引位置,首先在索引 i1 的桶中尝试删除 tag,如果成功找到并删除,计数 num_items_ 减 1,并跳到 TryEliminateVictim。
如果 i1 删除失败,则在 i2 的桶中尝试删除 tag。若找到并删除,num_items_ 减 1,并跳到 TryEliminateVictim。
TryEliminateVictim 方法会尝试清除一个受害者,如果存在一个受害者项也就是满了之后插入的第一个元素(victim_),它会尝试重新添加该受害者项到表中。然后设置 victim_.used 为 false,然后调用 AddImpl(i, tag) 将 victim_ 项放入其索引 i 位置如果上述两步均未成功,检查是否存在一个待处理的受害者项(victim_),如果该受害者项匹配 tag 并且其索引为 i1 或 i2,则清除 victim_ 并返回 Ok,表示删除成功。
布谷鸟过滤器能够替代布隆过滤器吗?
布谷鸟过滤器也有自己的缺陷,且目前还无法替代布隆过滤器:
- 布谷鸟过滤器要求存储空间必须为 2 的幂次,其容量计算的方式为:
upperpower2(std::max<uint64_t>(1, max_num_keys / assoc)), upperpower2函数用于计算大于或等于给定值 x 的最小的2的幂。 - 随着元素个数的增加,发生 kickout 的概率也会增加,导致元素插入时间变慢。
- 对于同一个元素,布谷鸟过滤器最多存储 $2 * k$ 次,k 为桶的容量,如果超过这个数,插入必将会失败。
- 布谷鸟过滤器删除的是指纹副本,而无法完全确定这个指纹是属于需要删除的元素的。
与其他过滤器的比较
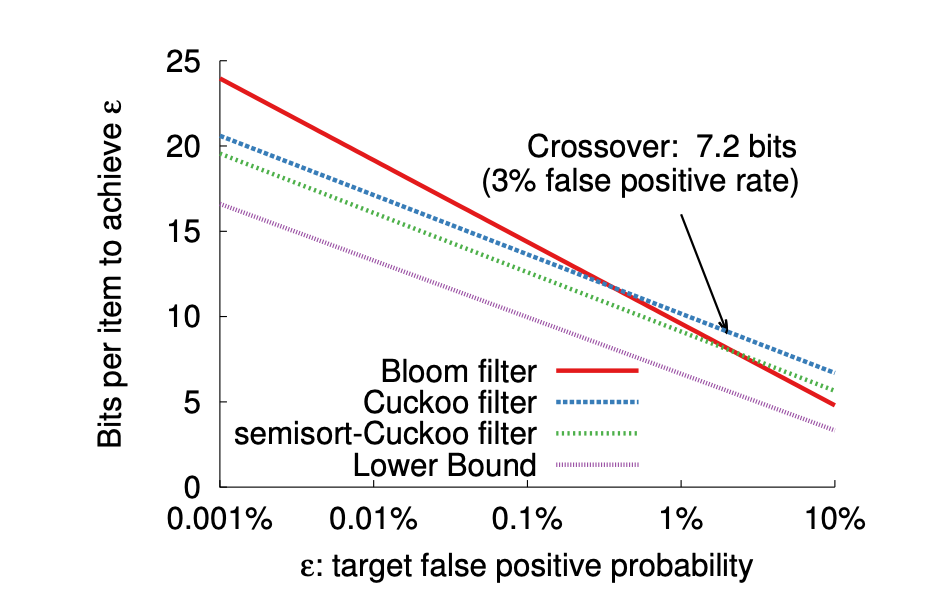
上图出自「Cuckoo Filter: Practically Better Than Bloom」,由此可知,布谷鸟过滤器在维护低误判率需要的空间成本上比布隆过滤器更低。
